General
The times series of GRACE+SLR CNES/GRGS RL05 solutions is provided in spherical harmonic coefficients up to degree and order 90.
Differences between RL04 and RL05
The main differences between our releases RL04 and RL05 are listed below:
‣ Latest version of L1B measurements (JPL v3 measurements);
‣ GPS constellation: IGS orbits and clocks are used instead of GRGS ones;
‣ All arcs start at the ascending node;
‣ Minimization of the data losses when there are interruptions within an arc (accelerometer data gaps, quaternion problems, on about 700 arcs);
‣ New model of ocean tides FES2014b;
‣ New linear mean pole model according to the latest IERS2010 Conventions;
‣ Suppression of the inhomogeneous relative weighting between KBR and GPS data affecting RL04-v1;
‣ Update of the inversion method, following the method used for the 10-day solution of RL04-v1: double reduction, with different constraint for the Cholesky step and for the SVD step.
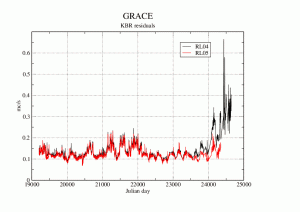
Comparison of K-Band-Range-Rate residuals between RL04 and RL05
A more detailed description of the RL05 processing is given thereafter.
Data
The version of the Grace data used for RL04 is L1B-v3.
The data from the Star Camera Assembly (SCA), Accelerometer (ACC), K-Band Ranging (KBR) and GPS receiver are used. The KBR data is processed in the form of the relative velocity between the spacecrafts: K-Band Range-Rate (KBRR).
In addition to the data from GRACE, the data from 5 SLR satellites are also used (Lageos, Lageos-2, Starlette, Stella and Ajisai), in order to provide an accurate and consistent description of the very low degrees of the gravity field (mainly degrees 1 and 2). As a consequence, there is a solution for degree 1 in the CNES/GRGS time series (coming from the SLR data) and there is no need to substitute the degree 2 coefficients by another set coming from an external source. The determination of degree 2 from the combination of the SLR and GRACE data is self-consistent with the rest of the other coefficients of the solution.
GRACE data:
KBR L1B-v3 data
Standard arc duration: 1 day
KBRR weighting:
- 0.1 μm/s + cos(φ) downweighting
GPS data:
- data sampling: 30ʺ
- data weighting: σcode = 100 cm, σphase = 2 cm
Parameters:
- Accelerometer biases: 1/half-revolution, piece-wise linear, on each axis
- Accelerometer scale factors: 1/day, constant, on each axis
- KBRR measurements: 1 bias + 1 slope per half-revolution, piece-wise linear
- KBR phase centers: 1/day Y & Z coordinates, for each sat
SLR data:
- Lageos1/2 data (10-day arcs, σapriori = 6 mm)
- Starlette/Stella/Ajisai data (5-day arcs, σapriori = 10 mm)
Gravity parameters:
- Gravity spherical harmonic coefficients complete to degree and order 90 (truncated to 30 for LAGEOS and 40 for GPS data)
- Ocean tides s. h. coefficients for 14 tidal waves with maximum degree/order ≤ 30 (not yet available)
A priori models
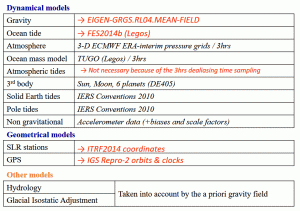
Note: For the GRACE Follow-On period, we use the official AOD1B RL06 dealiasing fields for atmosphere and ocean mass model instead of ERA-interim and TUGO.
Inversion method
By contrast with the GRACE solutions in spherical harmonics provided by other groups, the CNES/GRGS solutions are not obtained by a simple Cholesky inversion. The normal matrices are first diagonalized, ordered by decreasing order of the eigen values and only the best defined sets of linear combinations of the spherical harmonics are solved.
Since the gravity field is complete to degree and order 90, there are 91×91 = 8281 spherical harmonics coefficients and therefore 8281 linear combinations of spherical harmonics once the diagonalization is performed. On these 8281 linear combinations, 1500 are always solved without any constraint, approximately 2500 are solved with a progressive constraint towards their a priori value and the rest is left unsolved, i.e. is kept to its a priori value.
We estimate this inversion method allows to obtain a better spatial definition of the solutions, while keeping a low level of noise, than the classical Cholesky inversion up to the maximum degree of the gravity field, which must be followed by a spatial filtering in order to be usable.
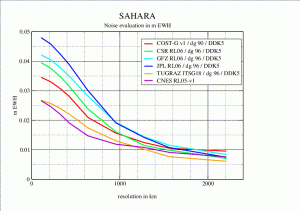
Below is plotted of an estimate of the residual noise, in m EWH, of different monthly solutions over the Sahara desert as a function of the spatial resolution expressed in km. Recent models, filtered by DDK5, are compared to CNES/GRGS RL05 solution, unfiltered.