Processing of SLR Observations at CNES
Due to the high level of uncertainty of the GRACE-only solutions for the degree 2 of the gravity field, the addition of Satellite Laser Ranging (SLR) data from dedicated geodetic satellites is necessary. For that purpose, the data from 4 SLR geodetic satellites (LAGEOS-1, LAGEOS-2, Starlette and Stella) are processed at CNES.
The data are processed in 5-day arcs and then cumulated per month or per 10-day periods, depending on the temporal resolution required. In addition to the gravity coefficients, the empirical dynamical parameters that are solved are: 1 drag parameter every 6 hours plus 1 periodic once-per-rev parameter along-track and 1 solar pressure parameter per arc for Starlette and Stella. For LAGEOS-1 and LAGEOS-2, which are sensitive to minute accelerations, one constant along-track parameter is solved-for per arc as well as one solar pressure parameter per arc. In addition, the Yarkovsky-Schach effect is taken into account for those satellites through one set of constant empirical accelerations in the orbital plane per arc (one acceleration along the line of nodes and one, in the orbital plane, perpendicular to the line of nodes). The Yarkovsky-Schach effect comes from the spin of these spherical satellites and the fact that, under the heating of the sun, one of their hemispheres becomes warmer than the other, thus producing a small radiative acceleration directed along their spin axis. The measurement parameters that are solved are one SLR range bias per station and per arc. Using the ITRF2014 for the station coordinates and EIGEN-GRGS.RL03-v2.MEAN-FIELD for the a priori gravity field, the mean SLR residuals are 8.4 mm for Lageos, 8.0 mm for Lageos-2, 10.5 mm for Starlette and 10.4 mm for Stella.
The CNES/GRGS SLR-only solutions between 2002 and 2016 for degrees 1 and 2 (quadratic mean pole convention) can be downloaded from :
CNES-GRGS.SLR-only.v2.monthly.coeff.tar.gz
In the case of the CNES/GRGS GRACE solutions, we do not substitute the SLR time series of the C(2,0) coefficient, but we add the SLR normal equations to the GRACE ones, before solving for the parameters, thus obtaining a combined solution for the very low degrees of the gravity field.
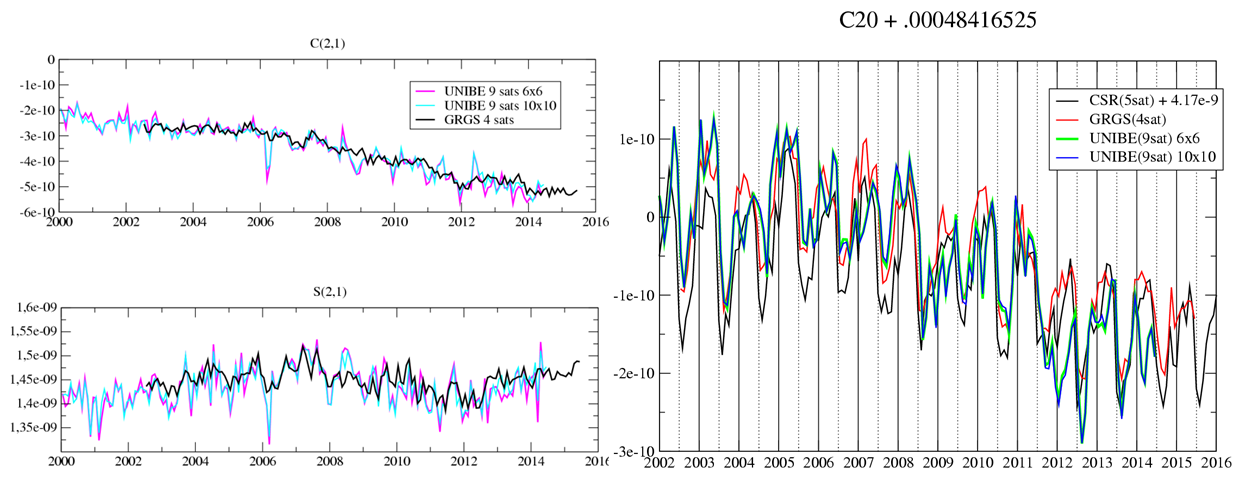
The time series of gravity coefficients for spherical harmonics degree 1 and degree 2, from SLR-only solutions, can be compared with those of other groups. For example in the Figures below, C(2,1) and S(2,1) from CNES/GRGS (based on 4 SLR satellites) are compared to those obtained at Bern University with 9 SLR satellites, and the C(2,0) coefficient is also compared to the time series provided, through Technical Note 07, by CSR (based on 5 SLR satellites) for substitution in the RL05 GRACE solutions (Cheng, M.K., B. D. Tapley, and J. C. Ries, « Deceleration in the Earth’s oblateness », Jour. Geophys. Res., V118, 1-8, doi:10.1002/jgrb.50058, 2013).